走进数学学院（三）

漫步π道，探索数字奥秘

NO.1 π道绵延

有一条路，和所有路都不一样。

你看不到它的尽头，沿途的风景也从不重复。

它是π道，也是数学之道。

NO.2 拨开π的迷雾

第一篇章 初见

人们对于圆周率π的理解经历了一个相当漫长的过程，从π的出现到确定它是无理数，人类花了近4千年的时间。

最早关于圆周率的历史记录可以追溯到约公元前20世纪，一块古巴比伦石匾清楚地记载了圆周率π=25/8=3.125。

同一时期的古埃及文物，莱因德数学纸草书也表明圆周率等于分数16/9的平方，约等于3.1605，埃及人似乎在更早的时候就知道圆周率了。

第二篇章 朦胧

英国作家John Taylor（1781-1864） 在其名著《金字塔》中指出，造于公元前2500年左右的胡夫金字塔和圆周率有关。例如，金字塔的周长和高度之比等于圆周率的两倍，正好等于圆的周长和半径之比。公元前800至600年成文的古印度宗教巨著《百道梵书》也显示了圆周率等于分数339/108，约等于3.139。

一直到公元前3世纪，古希腊著名数学家、物理学家阿基米德才将圆周率正确地计算到小数点后3位。此后经过五百多年的时间，魏晋时期中国数学家刘徽才将π值从3.141推进到3.14159。

刘徽是我国最早刻画圆周率的数学家，他利用割圆术，内接96边形得到π=3.1416。

又过了两百多年，南北朝时期的数学家祖冲之,发扬刘徽的割圆术,得到圆周率的范围3.1415926<π<3.1415927 ,被称之为"祖率"，并创立了π的两个分数形式,其中22/7称为约率,355/113称为密率.以此将π的精度计算到小数点后7位，并且在之后的800多年里祖冲之计算出的π值都是准确的。

第三篇章 逐渐明朗

一直到15世纪初阿拉伯数学家卡西求得圆周率17位精确小数值，打破祖冲之保持近千年的纪录。德国数学家鲁道夫·范·科伊伦于1596年将π值算到20位小数值，后投入毕生精力，于1610年算到小数后35位数，该数值被用他的名字称为鲁道夫数。

  此后，圆周率π的计算从几何法时期进入到分析法时期。这一时期人们开始利用无穷级数或无穷连乘积求π，摆脱可割圆术的繁复计算。无穷乘积式、无穷连分数、无穷级数等各种π值表达式纷纷出现，使得π值计算精度迅速增加。第一个快速算法由英国数学家梅钦提出，1706年梅钦计算π值突破100位小数大关，他利用了如下公式：

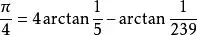
其中arctan x可由泰勒级数算出，类似的方法称为“梅钦类公式”。斯洛文尼亚数学家Jurij Vega于1789年得出π的小数点后140位，其中只有137位是正确的，这个世界纪录维持了五十年。到1948年英国的弗格森和美国的伦奇共同发表了π的808位小数值，成为人工计算圆周率值的最高纪录。

第四篇章 雾散

再后来，电子计算机的出现使π值的计算有了突飞猛进的发展。1949年，美国制造的世上首台计算机—ENIAC（电子数字积分计算机）在阿伯丁试验场启用了。次年，里特韦斯纳、冯纽曼和梅卓普利斯利用这部电脑，计算出π的2037个小数位，这部电脑只用了70小时就完成了这项工作。

五年后，IBM NORC（海军兵器研究计算机）只用了13分钟，就算出π的3089个小数位。科技不断进步，电脑的运算速度也越来越快，在60年代至70年代，随着美、英、法的电脑科学家不断地进行电脑上的竞争，π的值也越来越精确。在1973年，Jean Guilloud和Martin Bouyer以电脑CDC 7600发现了π的第一百万个小数位。

1976年，新的突破出现了。萨拉明（Eugene Salamin）发表了一条新的公式，那是一条二次收敛算则，也就是说每经过一次计算，有效数字就会倍增。高斯以前也发现了一条类似的公式，但十分复杂，在那没有电脑的时代是不可行的。这算法被称为布伦特-萨拉明（或萨拉明-布伦特）演算法，亦称高斯-勒让德演算法。

1989年美国哥伦比亚大学研究人员计算出π值小数点后4.8亿位数，后又继续算到小数点后10.1亿位数。2010年1月，法国工程师法布里斯·贝拉将圆周率算到小数点后2万7千亿位。2010年8月，日本计算机奇才近藤茂利用家用计算机和云计算相结合，计算出圆周率到小数点后5万亿位。一年后，近藤茂又刷新了之前5万亿位的记录，将圆周率计算到了小数点后10万亿位。

去年圆周率日（3月14日），谷歌工程师Emma Iwao利用谷歌运算引擎计算出精确度达31.4万亿位的圆周率。

NO.3 漫步林荫π道

小数假期时偷偷地在数学楼附近埋下的“小彩蛋”已经介绍的差不多了，现在只剩下π道和新完工的π雕啦！相信很多细心的同学也早就发现了这条绘满数字的林荫小道，以及数学楼前朴实无华的雕塑。今天就让小数来给大家介绍一下！

首先是位于求实路往数学楼方向的π道，从南区东门进来，往数学楼走，很快就能看到“I♡数学”的打卡标识牌，旁边就是我们的π道的起点了。π道从起始点开始，用艺术的字体记录着我们熟悉的圆周率——3.141592…

然后沿着π道一直走，就到达我们熟悉的数学楼，在这里有小数给大家新准备的一个“惊喜”——π雕。薄荷绿的配色在不失稳重的同时，又为数学楼外增添了几分活力。在介绍的最后，也希望小数精心准备的一切能够让刚刚回归校园或初入吉大的你眼前一亮！

启示

如今人们对圆周率的计算达到了小数点后30多万亿位，到了现在，它算到后面具体是什么数字已经不重要了，重要的是，小小的一个π，在人类文明发展史中引领我们不断探索的步伐。

人类对圆周率的探索正如这π道一样，道路是艰难的，人类在这条路上的第一步走了上千年，但每一步的前进都意味着人类工具、思想和智慧的进化，实验、几何法、分析法、计算机，人类计算圆周率的方法越来越高明，小数点后一位、两位、三位……，一位位数字的精确，一步步的前进，前辈们在这π道上不断思考和不断追求的精神闪耀着无限光辉，激励着我们向着更深处探寻，π道的尽头是什么，谁也不知道，但对于真理的探寻，我们不会停下脚步。