走进数学学院(二)
驻足碑前,欣赏欧拉公式之美
数学王国是充满奥秘的
如果把数字比作砖块
那么公式就是图纸
让我们一起来看看数学中最美的公式
欧拉公式
被誉为“上帝公式”
欧拉公式
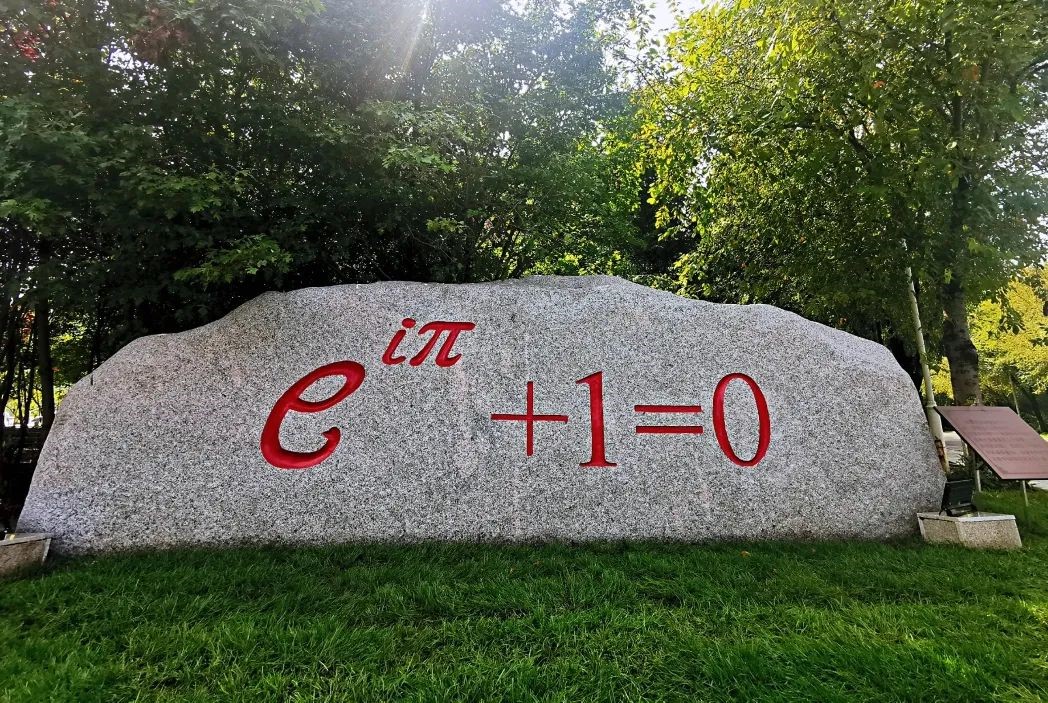
这个恒等式叫做欧拉公式,它是数学里最令人着迷的一个公式,它将数学里最重要的几个数字联系到了一起:两个超越数:自然对数的底e,圆周率π;两个单位:虚数单位i和自然数的单位1;以及被称为人类伟大发现之一的0。数学家们评价它是“上帝创造的公式”。
欧拉公式是指以欧拉命名的诸多公式。其中最著名的有:复变函数中的欧拉幅角公式——将复数、指数函数和三角函数联系起来,拓扑学中的欧拉多面体公式,初等数论中的欧拉函数公式。此外还包括其它一些欧拉公式,如分式公式等。
欧拉,18世纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把整个数学推至物理的领域。让我们先一起来了解一下欧拉的生平。
欧拉

莱昂哈德·欧拉(Leonhard Euler ,1707年4月15日~1783年9月18日),瑞士数学家、自然科学家。1707年4月15日出生于瑞士的巴塞尔,1783年9月18日于俄国圣彼得堡去世。欧拉出生于牧师家庭,自幼受父亲的影响。13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。欧拉是18世纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把整个数学推至物理的领域。他是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等的课本,《无穷分析引论》、《微分学原理》、《积分学原理》等都成为数学界中的经典著作。
欧拉对数学的研究如此之广泛,因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理。此外欧拉还涉及建筑学、弹道学、航海学等领域。瑞士教育与研究国务秘书Charles Kleiber曾表示:“没有欧拉的众多科学发现,我们将过着完全不一样的生活。” 法国数学家拉普拉斯认为:读读欧拉,他是所有人的老师。
欧拉公式的推导
问题来了,这么厉害的欧拉公式是怎么推导出来的呢?这就无法绕过一个知识——泰勒公式。
欧拉最早是从泰勒公式观察出欧拉公式的:
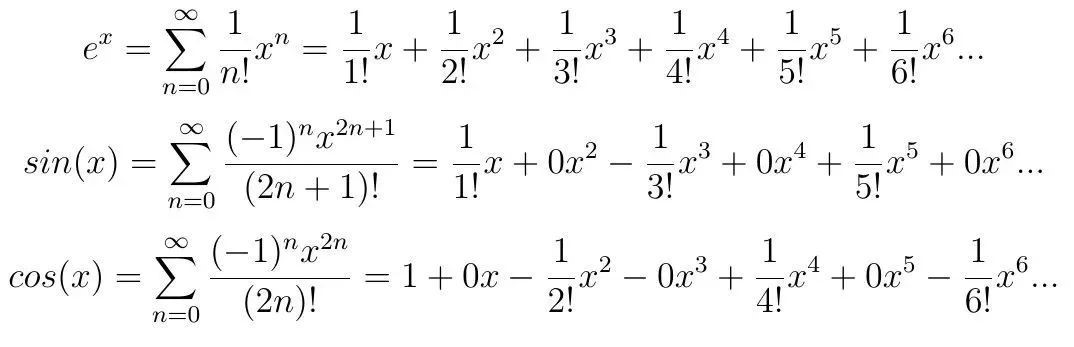
我们将x = iθ代入第一个泰勒展开式,可以得到:
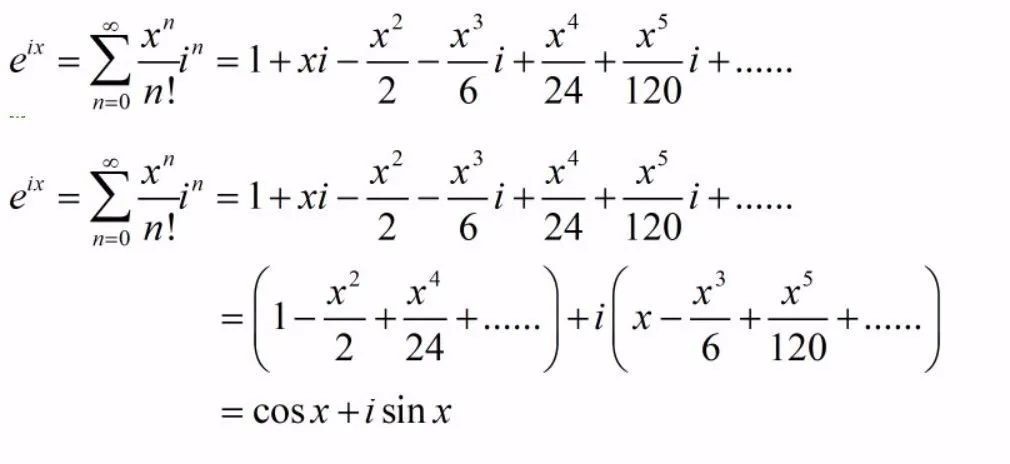
于是,我们就可以得到欧拉公式:
e^ix=cosx+i sinx
注意哦,这时候令x = π,化简,就得到了欧拉恒等式:
e^iπ + 1=0

这就得出了最美的公式之一,欧拉公式能够把e、π、i、1、0这五个简单而重要的数字联系在一起,其mathematic的美学因素显而易见,那就是----简洁!粗略一看可能不能看出任何花哨,但在数学爱好者眼中,它直接联系了指数函数,三角函数,复数,被称为“数学中的天桥”。
欧拉公式的美

之所以说它美,是因为这个公式的精简。它没有多余的字符,却联系着几乎所有的数学知识。
1.自然界的 e 含于其中
自然对数的底,大到飞船的速度,小至蜗牛的螺线,谁能够离开它?
2.最重要的常数 π 含于其中
世界上最完美的平面对称图形是圆。“最伟大的公式”能够离开圆周率吗?(还有π和e是两个最重要的无理数!)
3.最重要的运算符号 + 含于其中
之所以说加号是最重要的符号,是因为其余符号都是由加号派生而来。减号是加法的逆逆运算,乘法是累计的加法……
4.最重要的关系符号 = 含于其中
从你一开始学算术,最先遇见它,相信你也会同意这句话。
5.最重要的两个元在里面
零元0,单位元 1是构造群,环,域的基本元素。如果你看了有关《近世代数》的书,你就会体会到它的重要性。
6.最重要的虚单位 i 也在其中
虚单位 i 使数轴上的问题扩展到了平面,而在哈密尔的 4元数与凯莱的8元数中也离开不了它。
有了加号,可以得到其余运算符号;有了0,1,就可以得到其他的数字;有了 π就有了圆函,也就是三角函数;有了 i 就有了虚数,平面向量与其对应;也就有了哈密尔的4元数,现实的空间与其对应;有了 e 就有了微积分,就有了和工业革命时期相适宜的数学。


数学
是连接世界的密码
是一切自然的解答
捧起物理的星河千万
亲吻生化的配平统筹
数学的答案没有尽头


通往数学楼的路上新建了一个石碑,上面印着数学里面最美的公式——欧拉公式。
大家可以去感受一下,走走π道,看看最美的数学公式。
说不定,一下子想明白了困扰了很久的问题。
这,就是属于数学的魅力吧!